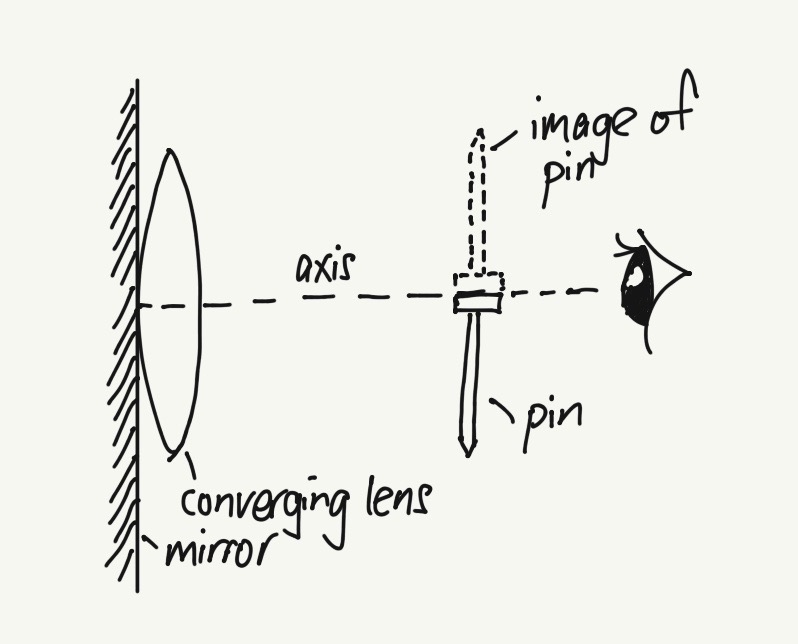
A thin convex lens is placed on a plane mirror and an object pin is then moved along the axis of the lens until an image is seen to coincide with the object pin when viewed from above. What is then the distance between the pin and the lens? (Take f as the focal length of the lens)
A 0.5 f B 1.0 f C 1.5 f D 2.0 f
Answer: Option B
A common mistake is to assume this is the scenario (2nd scenario) where the object is at 2F and the image formed is at 2F, hence the image is the same size as the object, inverted and real. But this is not the case.
Refer to the video tutorial for the explanation.
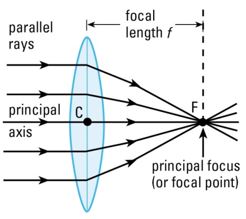
This set up of the lens with the mirror is using the concept that when parallel light rays (parallel to principal axis) enter the lens, the rays will converge to a point after passing through the lens. This point is called the focal point, F. The distance between F and the optical center of lens is the focal length f. Refer to the diagram below.
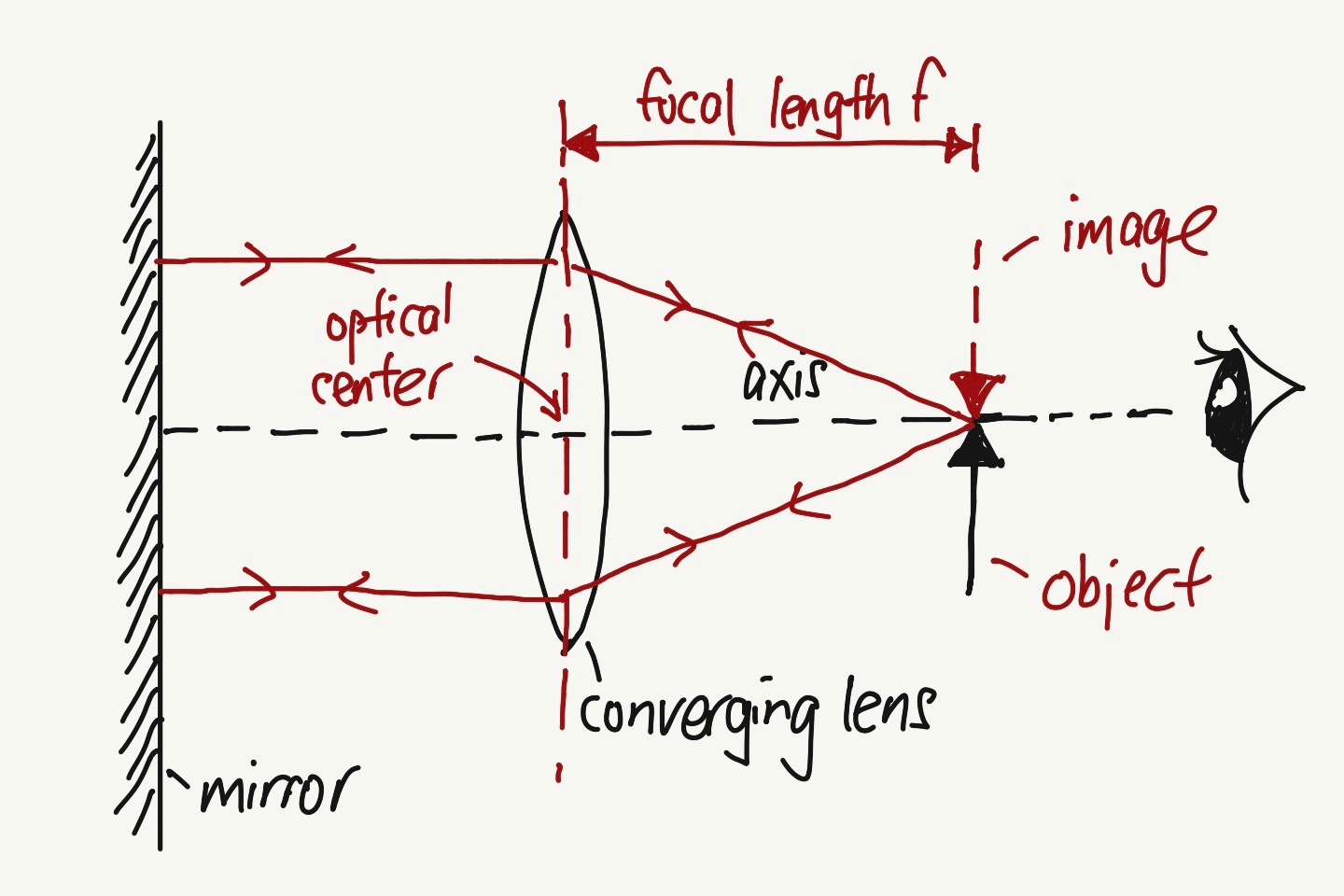
When you adjust the object (pin) until both the object and the image coincide even when you move your eye forward or backward perpendicular to the axis, the distance between the optical center and the object (pin) is the focal length f.
At this position, as the rays from the object pass through the lens, due to refraction, the rays converge and becomes parallel to the axis. Due to the mirror, the parallel rays will be reflected back to the lens and then converge to a point that coincides with the object.
Refer to the video on how to get that position.
Before you start the experiment to find the focal length f, there is a fast and easy way to estimate the f. Refer to the video below.
Below is another image of another set-up but with the same concept.
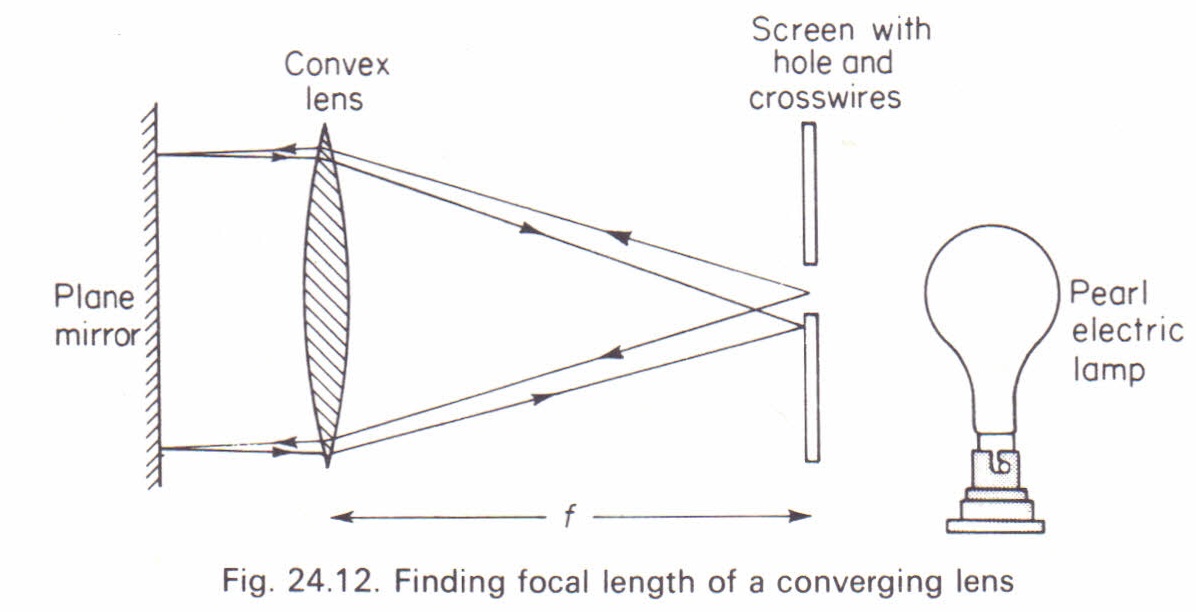
Another similar question below. The answer is Option B
Click here to view the post on a typical lens experiment and things to take note.
Another experiment which involved the same technique. Pins inside and outside the beaker of water

Pingback: Converging Lens Overview | Evan's Space