Video 01: The various physical quantities in kinematics
Video 02: Acceleration
Video 03: Graphical Analysis of Motion (Displacement (distance)-Time Graph and Velocity (speed)-Time Graph)
Video 04: Describing the motion of the car – practice
Video 05: Free-fall, acceleration due to gravity
Video 06: Motion of 2 objects
1) When a ball is thrown up and it comes down
When the ball leaves the hand, there is no upward force acting on the ball. The only force acting on the ball is its weight. This net force is opposite to the motion of the ball, hence causing the ball to decelerates. Refer to this post for the explanation (comics)
3) When the ball is dropped and it re-bounces back (in reality with energy lost)
In reality, when the ball hits the ground, there will be some energy converted to heat and sound. So the ball will never return to its original height that it was released. So how will the graphs look like?
When a ball is thrown up vertically from a height and the falls to the ground, the various kinematic graphs below shows the same motion of the ball.
Fixing up as positive, if the ball is going up, it’s displacement and velocity will be in the positive region. When it falls, the direction is opposite, hence it’s in the negative portion.
Recall that the gradient of a velocity-time graph represents the acceleration. Using this concept, it will be easier to understand that the acceleration is a negative constant acceleration, thus – 10 ms-2.
(Thanks Maria for suggesting this post and the addition of acceleration-time graph)
Click here to refer to the post related to this motion.
Velocity-time and Displacement-time Graph for a ball being thrown up
Velocity-time and Displacement-time graph for Ball thrown up and comes down
When a ball is released from a height, it will accelerate on the way down due to the resultant force (weight) acting downwards. Just before the ball touches the ground, the velocity of the ball is the maximum. When it hits the ground, the speed decreases to 0 m/s instantly. When it rebounces back in the opposite direction, the initial velocity is the maximum. Assume ideal situation (no air resistance, no energy lost to sound or heat). The ball will rebounce back to its original height.
In reality, there is work done against air resistance, energy converted to heat and sound when ball hits the ground, hence the ball will never reach its original height.
Note that in both situations, conservation of energy always applied. All energy is conserved, just that energy of the ball is converted to other forms like heat and sound.
Click here to view a comic on forces explanations of ball thrown up
Click here to view the post on velocity-time and displacement-time of ball thrown up
A ball is thrown vertically upwards from the hand and lands back onto the hand. It is important to note that once the ball leaves the hand, the  resultant force acting on the ball is only its weight! And it is acting downwards throughout the motion.Â
Velocity-Time Graph
Displacement-Time Graph
Key points to note when sketching the v-t graph:
1) Fixing the direction up to be positive (can be down as positive if you want)
2) At t = 0s, the initial velocity of the ball is maximum.
3) As it goes up vertically, due to the weight acting downwards, the ball decreases in speed (decelerates)
4) At the highest point, the ball is momentarily at rest (v =0m/s)
5) On the way down, due to the weight of the ball acting downward, the ball accelerates downwards.
A stone is dropped from a bridge 2.0 m above the roof of a train moving horizontally below. The train is travelling at a uniform speed of 30.0 m/s. What distant is covered by the train as the stone falls? (Take g =Â 10 m/s2)
The train is moving to the left at a constant speed. We just need to find the time taken for the ball to fall 2 m. Â This is normal free fall of ball. Recall: when distance is given, think of area under the graph. Once time is found, the distance travels by the train can be easily found.
If the train is accelerating constantly, would you be able to solve?
At t = 0s, both cars are at Line 1. Car A is moving at constant speed of 20 m/s, while Car B is moving off from rest with a initial constant acceleration and then maintains at a constant speed of 25 m/s after t = 15s. Line 2 is 500 m away from Line 1.
a) Sketch the motion of both cars on a speed-time graph.
b) What is the time taken for Car A to reach Line 2?
c) What is the time taken for Car B to reach Line 2?
d) If both cars maintain their constant speeds, Car B will overtake Car A eventually. At what time and distance from Line 1 will Car B overtakes Car A? Â
Solutions:
a) To solve such questions, even though graph is not required, it is useful to sketch out the speed-time graph for better visualisation.
b) Whenever given distance travelled by car, it is always good to think of area under the graph.
c) Distance covered is still 500 m, which is the area under the graph.
d) As Car B is travelling with a greater constant speed, eventually it will overtake. But when? Definitely after 15s? Or possible to be before 15s?
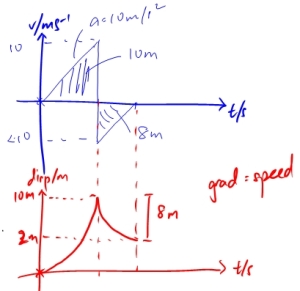
A 10 kg box is initially at rest on a rough horizontal surface and a horizontal force is then applied to it. The force varies as shown in the diagram.
a) If the box moves with an acceleration of 2m/s2 in the first 15 s, what is the frictional force between the surfaces?
Resultant force on box = ma
Applied force – frictional force = ma
40 – frictional force = 10 x 2
frictional force = 20 N
b) How does the velocity change during the next 5 s?
Next 5 s after time 15 s, there is no applied force. Hence the resultant force acting on box isonly frictional force 20N (in direction opposite to motion of box).
F = ma
-20 = 10 x a
a = – 2 m/s2
The velocity of box at time 15s is required.
Hence when t = 0s, box accelerates at 2m/s2 from rest,
a = (v – u) / t
2 = (v – 0) /15
v = 30 m/s
(Hence the final velocity of the box at time 15s is 30 m/s, just before applied force of 40 N is released)
Find velocity of box at end of next 5s (time = 20s):
a = (v – u) /t
– 2 = (v – 30) / 5
v = 20 m/s.
Therefore, velocity decreases at a constant rate of -2 m/s2 from 30 m/s to 20 m/s in next 5s.
c) Plot a velocity-time graph and calculate the distance travelled by the box in the 30 s.
A boy of mass 40 kg jumps from rest from a platform of height 3 m. He lands by bending his knees and stops his body in 0.5 s after landing. What is the force exerted by his legs? 
Solutions: 620 N
To solve this question, you need to apply conservation of energy (COE) to find the kinetic energy (KE) that the boy possesses just before he reaches the ground.
After which, you can solve the question using (1) Conservation of energy or (2) Kinematics to solve.
Using COE to find the KE just before he reaches the ground.
Method 1: Using Conservation of Energy (COE)
Method 2: Using Kinematics
Evan's Space 